Лекция по математике на тему "признак перпендикулярности двух плоскостей". Стереометрия Две плоскости называются перпендикулярными

Тема урока: «Признак перпендикулярности двух плоскостей»

Тип урока: Урок изучения нового материала

Формируемые результаты:

Предметные: ввести понятие угла между плоскостями, познакомить учащихся с определением перпендикулярных плоскостей, признаком перпендикулярности двух плоскостей, формировать умение применять его при решении задач.

Личностные: развивать познавательный интерес к геометрии, формировать умение представлять результат своей деятельности.

Метапредметные: формировать умение ставить и формулировать для себя новые задачи в учебе и познавательной деятельности.

Планируемые результаты: учащийся научится применять новую теорему при решении несложных задач.

Оборудование: доска, готовые рисунки (слайд-фильм), модели, изготовленные учащимися и учителем, текст задачи на печатной основе.

Cлова Пойа Д.:

Подробнее во вложении

Скачать:

Предварительный просмотр:

Урок геометрии в 10 классе.

Тема урока: «Признак перпендикулярности двух плоскостей»

Тип урока: Урок изучения нового материала

Формируемые результаты:

Планируемые результаты: учащийся научится применять новую теорему при решении несложных задач.

Cлова Пойа Д.: «Нужно всеми средствами обучать искусству доказывать, не забывая при этом и об искусстве догадываться».

1. Оргмомент.

2. Проверка домашнего задания.

1)Ученик с моделью двугранного угла рассказывает, как образуется его линейный угол; дает определение градусной меры двугранного угла.

2) Задача №1. (Слайд 2) – по рисунку.

3) Задача №2. (Слайд 3) – по рисунку.

К этим задачам вернемся позже перед доказательством признака.

3. Актуализация знаний.

1) Рассказ ученика о пересекающихся плоскостях (используется модель).

2) Определение перпендикулярных плоскостей (использует модель), примеры.

Вернемся к домашним задачам. Было установлено, что в обоих случаях двугранные углы равны 90°, т.е. являются прямыми. Посмотрим, какие символы нужно вставить вместо точек и сделаем вывод о взаимном расположении плоскостей (слайд 4).

(AFC) FO (ADC)

(AFC) (ADC).

Выясним, можно ли без нахождения двугранного угла сделать вывод о перпендикулярности плоскостей?

Обратите внимание на связь (слайд 5):

(DCC₁) DD₁ (ABC) (DCC₁) (ABC) и

(AFC) FO (ADC) (AFC) (ADC)

Формулирование предположения учащимися.

4. Изучение нового материала.

1). Сообщение темы урока: «Признак перпендикулярности двух плоскостей».

2). Формулировка теоремы (учебник): «Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны» ; показ на модели.

3). Доказательство проводится по заранее заготовленному чертежу (рис.62).

Дано: α, β – плоскости; α АВ β; АВ ∩ β = А

Доказать: α β.

Доказательство: 1) α ∩ β = АС

2) АВ АС (?)

3) Построим АD β; АD АС

4) L BAD - ……….. , L BAD = …. ° (?)

5) L (α, β) = 90°, т.е. α β.

5. Первичное закрепление (ПЗ).

1). Решение задачи 1 на готовом чертеже (слайд 6).

Дано: DА

Доказать: (DАС)

2). Решение задачи 2 на готовом чертеже + у каждого заготовленный вырезанный ромб (слайд 7).

Дано: АВСД – ромб;

Перегибаем по диагонали:

ВО

Докажи: (АВС)

3). Задача 3. «Слепой» текст на печатной основе (слайды 8-9).

Дано: рисунок; двугранный угол ВАСД – прямой.

Найди: ВД

Самостоятельно. Проверка.

6. Итоги урока. Информация о домашнем задании.

Данный урок поможет желающим получить представление о теме «Признак перпендикулярности двух плоскостей». В начале него мы повторим определение двугранного и линейного угла. Затем рассмотрим, какие плоскости называются перпендикулярными, и докажем признак перпендикулярности двух плоскостей.

Тема: Перпендикулярность прямых и плоскостей

Урок: Признак перпендикулярности двух плоскостей

Определение. Двугранным углом называется фигура, образованная двумя полуплоскостями, не принадлежащими одной плоскости, и их общей прямой а (а - ребро).

Рис. 1

Рассмотрим две полуплоскости α и β (рис. 1). Их общая граница - l. Указанная фигура называется двугранным углом. Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.

Двугранный угол измеряется своим линейным углом. На общем ребре l двугранного угла выберем произвольную точку. В полуплоскостях α и β из этой точки проведем перпендикуляры a и b к прямой l и получим линейный угол двугранного угла.

Прямые a и b образуют четыре угла, равных φ, 180° - φ, φ, 180° - φ. Напомним, углом между прямыми называется наименьший из этих углов.

Определение. Углом между плоскостями называется наименьший из двугранных углов, образованных этими плоскостями. φ - угол между плоскостями α и β, если

Определение. Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°.

Рис. 2

На ребре l выбрана произвольная точка М (рис. 2). Проведем две перпендикулярные прямые МА = а и МВ = b к ребру l в плоскости α и в плоскости β соответственно. Получили угол АМВ. Угол АМВ - это линейный угол двугранного угла. Если угол АМВ равен 90°, то плоскости α и β называются перпендикулярными.

Прямая b перпендикулярна прямой l по построению. Прямая b перпендикулярна прямой а, так как угол между плоскостями α и β равен 90°. Получаем, что прямая b перпендикулярна двум пересекающимся прямым а и l из плоскости α. Значит, прямая b перпендикулярна плоскости α.

Аналогично можно доказать, что прямая а перпендикулярна плоскости β. Прямая а перпендикулярна прямой l по построению. Прямая а перпендикулярна прямой b, так как угол между плоскостями α и β равен 90°. Получаем, что прямая а перпендикулярна двум пересекающимся прямым b и l из плоскости β. Значит, прямая а перпендикулярна плоскости β.

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Доказать:

Рис. 3

Доказательство:

Пусть плоскости α и β пересекаются по прямой АС (рис. 3). Чтобы доказать, что плоскости взаимно перпендикулярны, нужно построить линейный угол между ними и показать, что этот угол равен 90°.

Прямая АВ перпендикулярна по условию плоскости β, а значит, и прямой АС, лежащей в плоскости β.

Проведем прямую АD перпендикулярно прямой АС в плоскости β. Тогда ВАD -линейный угол двугранного угла.

Прямая АВ перпендикулярна плоскости β, а значит, и прямой АD, лежащей в плоскости β. Значит, линейный угол ВАD равен 90°. Значит, плоскости α и β перпендикулярны, что и требовалось доказать.

Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей (рис. 4).

Доказать:

Рис. 4

Доказательство:

Прямая l перпендикулярна плоскости γ, а плоскость α проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости α и γ перпендикулярны.

Прямая l перпендикулярна плоскости γ, а плоскость β проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости β и γ перпендикулярны.

Напомним, что плоскости называются перпендикулярными, если угол между ними прямой. А угол этот определяется так. Берут точку О на прямой С, по которой пересекаются плоскости , и проводят через нее в плоскостях прямые (рис. 1.9а). Углом между а и b и измеряется угол между . Когда этот угол прямой, то говорят, что плоскости взаимно перпендикулярны и пишут

Вы, конечно, уже заметили, что когда , то из трех прямых а, b, с любые две взаимно перпендикулярны (рис. 2.28). В частности, . Поэтому (по признаку перпендикулярности прямой и плоскости). Аналогично,

Итак, каждая из двух взаимно перпендикулярных плоскостей содержит перпендикуляр к другой плоскости. Более того, эти перпендикуляры заполняют взаимно перпендикулярные плоскости. (рис. 2.29).

Докажем последнее утверждение. Действительно, если через любую точку плоскости а провести прямую

То (по теореме 5 о параллельности перпендикуляров).

А для признака перпендикулярности плоскостей достаточно одного перпендикуляра к плоскости.

Теорема 7. (признак перпендикулярности плоскостей). Если плоскость проходит через перпендикуляр к другой плоскости, то эти плоскости взаимно перпендикулярны.

Пусть плоскость а содержит прямую а, перпендикулярную плоскости Р (рис. 2.28). Тогда прямая а пересекает плоскость Р в точке О. Точка О лежит на прямой С, по которой пересекаются . Проведем в плоскости Р через точку О прямую . Так как и b лежит в плоскости Р, то Следовательно,

Данный признак имеет простой практический смысл: плоскость двери, навешенной на перпендикулярный полу косяк, перпендикулярна плоскости пола при любых положениях двери (рис. 2.1). Другое практическое применение этого признака: когда требуется проверить, вертикально ли установлена плоская поверхность (стена, забор и т. п.), то это делают с помощью отвеса - веревки с грузом. Отвес всегда направлен вертикально, и стена стоит вертикально, если в любом ее месте отвес, располагаясь вдоль нее, не отклоняется.

При решении задач, в которых встречаются перпендикулярные плоскости, часто используются следующие три предложения.

Предложение 1. Прямая, лежащая в одной из двух взаимно перпендикулярных плоскостей и перпендикулярная их общей прямой, перпендикулярна другой плоскости.

Пусть плоскости взаимно перпендикулярны и пересекаются по прямой С. Пусть, далее, прямая а лежит в плоскости а и (рис. 2.28). Прямая а пересекает прямую С в некоторой точке О. Проведем через точку О в плоскости Р прямую b, перпендикулярную прямой с. Так как то . Поскольку , то (по теореме 2).

Второе предложение обратно первому.

Предложение 2. Прямая, имеющая общую точку с одной из двух взаимно перпендикулярных плоскостей и перпендикулярная другой плоскости, лежит в первой из них.

Пусть плоскости взаимно перпендикулярны, прямая а также прямая а имеет с плоскостью а общую точку А (рис. 2.30). Через точку А в плоскости а проведем прямую перпендикулярную прямой С - линии пересечения плоскостей . Согласно предложению Поскольку в пространстве через каждую точку проходит лишь одна прямая, перпендикулярная данной плоскости, то прямые а и совпадают. Так как лежит в плоскости а, то и а лежит в плоскости

Предложение 3. Если две плоскости, перпендикулярные третьей плоскости, пересекаются, то прямая их пересечения перпендикулярна третьей плоскости.

Пусть две плоскости , пересекающиеся по прямой а, перпендикулярны плоскости у (рис. 2.31). Тогда через любую точку прямой а проведем прямую, перпендикулярную плоскости у. Согласно предложению 2, эта прямая лежит и в плоскости а, и в плоскости Р, т. е. совпадает с прямой а. Итак,

Перпендикулярность плоскостей Определение. Две плоскости называются перпендикулярными, если линейный угол при ребре двугранного угла между этими плоскостями - прямой.
Признак перпендикулярности плоскостей. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Доказательство. Пусть a и ? - две пересекающиеся плоскости, с - прямая их пересечения и а - прямая перпендикулярная плоскости ? и лежащая в плоскости a . А - точка пересечения прямых a и с. В плоскости ? из точки А восстановим перпендикуляр, и пусть это будет прямая b . Прямая а перпендикулярна плоскости ? , а значит она перпендикулярна и любой прямой в этой плоскости, то есть прямые b и с перпендикулярны. Угол между прямыми а и Ь - линейный плоскостями a и ? и равен он 90°, так как прямая а перпендикулярна прямой b (подоказанному).Поопределениюплоскости a и ? перпендикулярны.

Теорема 1 . Еслииз точки,принадлежащейодной из двух перпендикулярных плоскостей,провести перпендикуляр к другой плоскости, то это перпендикуляр полностью лежит в первой плоскости.
Доказательство. Пусть a и ? - перпендикулярные плоскости и с - прямая их пересечения, А - точка лежащаявплоскостиa и не принадлежащая прямой с. Пустьперпендикуляр к плоскости ? проведенный из точки А , не лежит в плоскости a , тогда точка С – основание этого перпендикуляра лежит в плоскости ? и не принадлежит прямой с. Из точки А опустим перпендикуляр АВ напрямую с. Прямая АВ перпендикулярна плоскости (использую теорему 2). Через прямую АВ и точку С проведем плоскость ? (прямая и точка определяют плоскость, причем только одну). Мы видим, что в плоскости ? из одной точки А на прямуюВС проведено два перпендикуляра, чего быть не может, значит прямая АС совпадает с прямой АВ, а прямая АВ в свою очередь полностью лежит в плоскости a .

Теорема 2 . Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
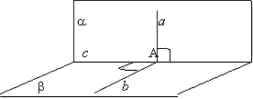Доказательство. Пусть a и ? - две перпендикулярные плоскости, с - прямая их пересечения и а - прямая перпендикулярная прямой с и лежащая в плоскости a . А - точка пересечения прямых а и с. В плоскости ? из точки А восстановим перпендикуляр, и пусть это будет прямая b . Угол между прямыми а и b - линейный угол при ребре двугранного угла между плоскостями a и ? и равен он 90°, так как плоскости a и ? перпендикулярны. Прямая а перпендикулярна прямой b (по доказанному) и прямой с по условию. Значит прямая а перпендикулярна плоскости? (

Понятие перпендикулярных плоскостей

При пересечении двух плоскостей у нас получается $4$ двугранных угла. Два угла равны $\varphi $, а два другие равны ${180}^0-\varphi $.

Определение 1

Углом между плоскостями называется минимальный из двугранных углов, образованных этими плоскостями.

Определение 2

Две пересекающиеся плоскости называются перпендикулярными, если угол между этими плоскостями равен $90^\circ$ (рис. 1).

Рисунок 1. Перпендикулярные плоскости

Признак перпендикулярности двух плоскостей

Теорема 1

Если прямая плоскости перпендикулярна другой плоскости, то эти плоскости перпендикулярны друг другу.

Доказательство.

Пусть нам даны плоскости $\alpha $ и $\beta $, которые пересекаются по прямой $AC$. Пусть прямая $AB$, лежащая в плоскости $\alpha $ перпендикулярна плоскости $\beta $ (рис. 2).

Рисунок 2.

Так как прямая $AB$ перпендикулярна плоскости $\beta $, то она перпендикулярна и прямой $AC$. Проведем дополнительно прямую $AD$ в плоскости $\beta $, перпендикулярно прямой $AC$.

Получаем, что угол $BAD$ - линейный угол двугранного угла, равный $90^\circ$. То есть, по определению 1, угол между плоскостями равен $90^\circ$, значит, данные плоскости перпендикулярны.

Теорема доказана.

Из этой теоремы следует следующая теорема.

Теорема 2

Если плоскость перпендикулярна прямой, по которой пересекаются две другие плоскости, то она перпендикулярна и этим плоскостям.

Доказательство.

Пусть нам даны две плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Плоскость $\gamma $ перпендикулярна прямой $c$ (рис. 3)

Рисунок 3.

Так как прямая $c$ принадлежит плоскости $\alpha $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\alpha $ и $\gamma $ перпендикулярны.

Так как прямая $c$ принадлежит плоскости $\beta $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\beta $ и $\gamma $ перпендикулярны.

Теорема доказана.

Для каждой из этих теорем справедливы и обратные утверждения.

Примеры задач

Пример 1

Пусть нам дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Найти все пары перпендикулярных плоскостей (рис. 5).

Рисунок 4.

Решение.

По определению прямоугольного параллелепипеда и перпендикулярных плоскостей видим следующие восемь пар перпендикулярных между собой плоскостей: $(ABB_1)$ и $(ADD_1)$, $(ABB_1)$ и $(A_1B_1C_1)$, $(ABB_1)$ и $(BCC_1)$, $(ABB_1)$ и $(ABC)$, $(DCC_1)$ и $(ADD_1)$, $(DCC_1)$ и $(A_1B_1C_1)$, $(DCC_1)$ и $(BCC_1)$, $(DCC_1)$ и $(ABC)$.

Пример 2

Пусть нам даны две взаимно перпендикулярные плоскости. Из точки одной плоскости проведен перпендикуляр к другой плоскости. Доказать, что эта прямая лежит в данной плоскости.

Доказательство.

Пусть нам даны перпендикулярные плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Из точки $A$ плоскости $\beta $ проведен перпендикуляр $AC$ к плоскости $\alpha $. Предположим, что $AC$ не лежит в плоскости $\beta $ (рис. 6).

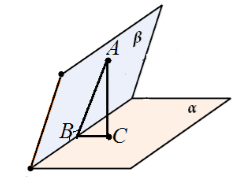
Рисунок 5.

Рассмотрим треугольник $ABC$. Он является прямоугольным с прямым углом $ACB$. Следовательно, $\angle ABC\ne {90}^0$.

Но, с другой стороны, $\angle ABC$ является линейным углом двугранного угла, образованного этими плоскостями. То есть двугранный угол, образованный этими плоскостями не равняется 90 градусам. Получаем, что угол между плоскостями не равен $90^\circ$. Противоречие. Следовательно, $AC$ лежит в плоскости $\beta $.